今天要講的資料結構叫做Trie，也可以稱作Prefix Tree，我認為他是一種比較進階的資料結構，所以我把它放到後面一點來介紹囉，

既然都叫作Prefix Tree那他一定跟樹長的很像拉，沒有錯喔，只是Prefix Tree有一個特別的用途，就是在做一些字串比對的時候會有不錯的時間複雜度。另外，我們打英文的時候，當我們打到特定長度的時候，會有一些推薦的字出現，那種效果也是透過Prefix Tree來實作的呦！

Array裡搜尋字串

想像今天我有這一些字 “me”, “meet”, “met”, “you”, “youtube”，我要存放起來以後搜尋用的，最直覺的方式就是存放在Array裡，現在當我要搜尋”met”這個字，我的時間複雜度會是多少呢？
首先，我們要先搜尋過整個Array裡頭的元素，這邊就要花O(n)，n是Array裡元素的數量，對於每一個字串，我們必須去比對字串是否相同，這邊會花O(m)，m是字串的長度，所以我總共的時間複雜度是O(mn)。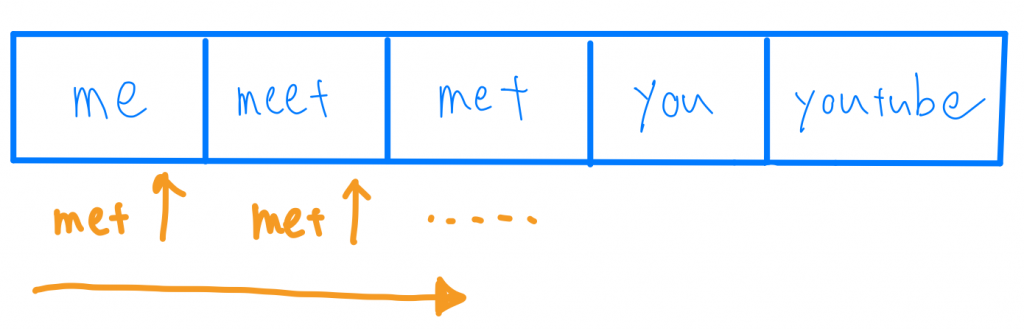

另外我們還會發現，met跟me跟meet前面的兩個字是相同的都是「me」開頭，這種方式，我們重複的紀錄了相同的部分。

更好的方式

有沒有更好的方式呢？當然有的，就是我們今天的主角Prefix Tree。
廢話不多說，我們看看一樣的資料我可以怎麼儲存在Prefix Tree上，直接上圖。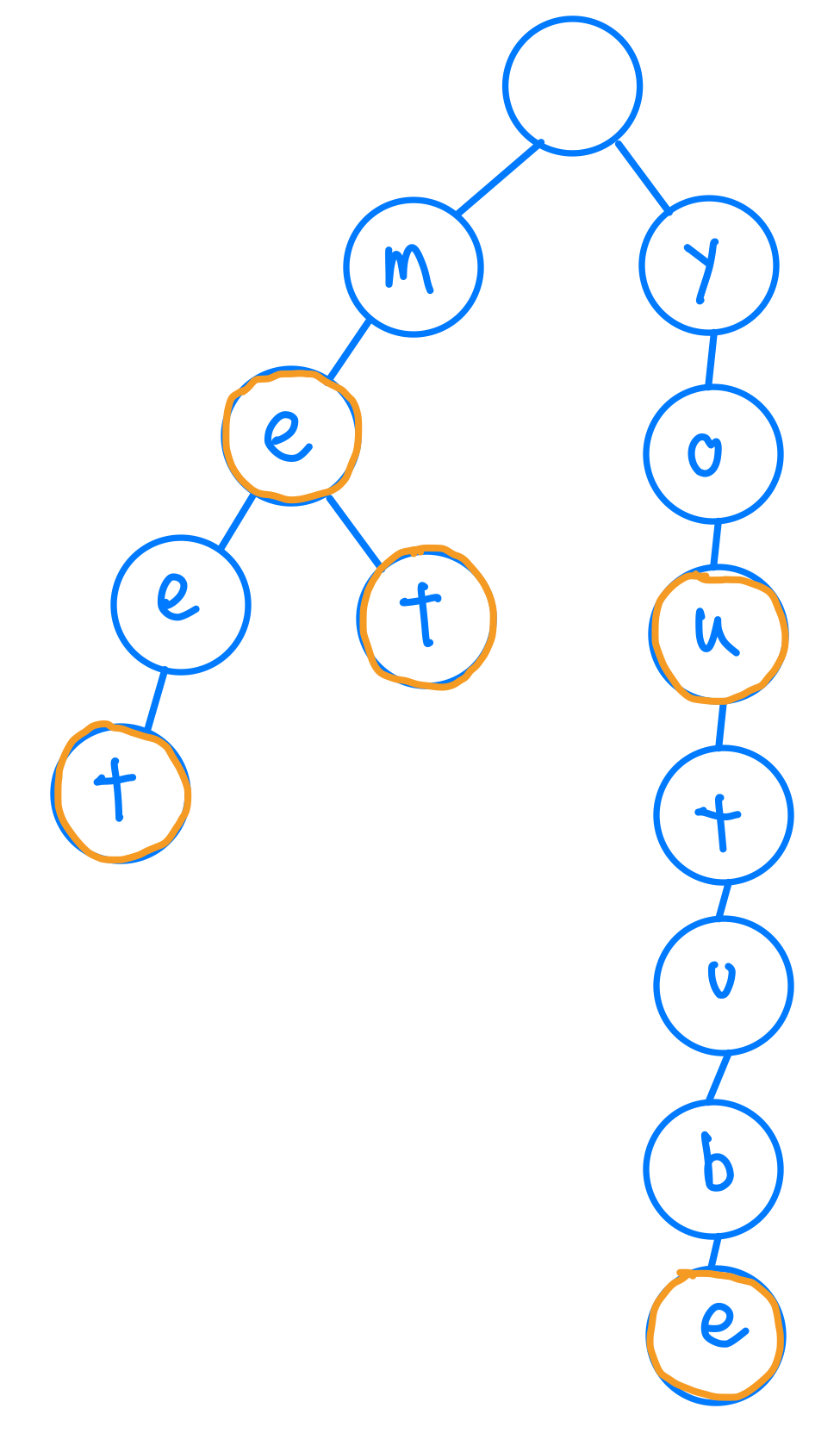

實作上，在python裡，我們會用dict也就是Hash Map來去記錄我的子節點，這樣我可以用in來去找我下一個字母有沒有存在。
這邊我們可以看到每一個節點就存放一個字母，這樣我們就不會重複儲存到前面的字母是一樣的這種情況，有一些節點我們是用橘色圈起來的，這種節點就帶表他是那個單字的最後一個字母，所以當我們要判斷單字存不存在，最後還要判斷該節點是不是橘色的，實作上我們可以利用Boolean值去紀錄即可。
我們來看看如果要搜尋特定的單字呢？因為我們是用HashMap的關係，我們可以用in的operation來去往下一個節點走，in是O(1)的時間複雜度，我們最多會in字串的長度這麼多次，所以時間複雜度是O(m) ，m是字串的長度，是不是優化了許多呢？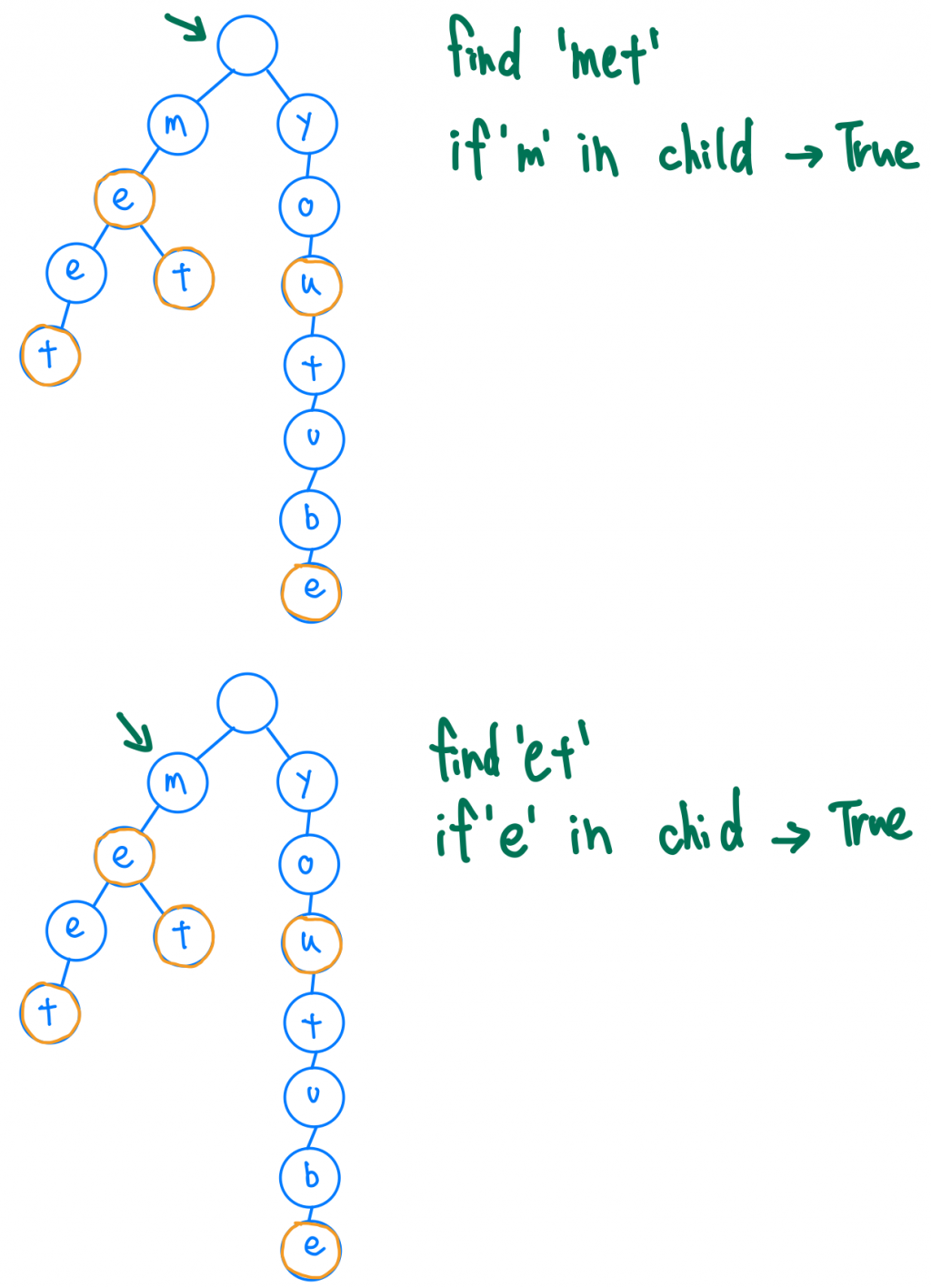

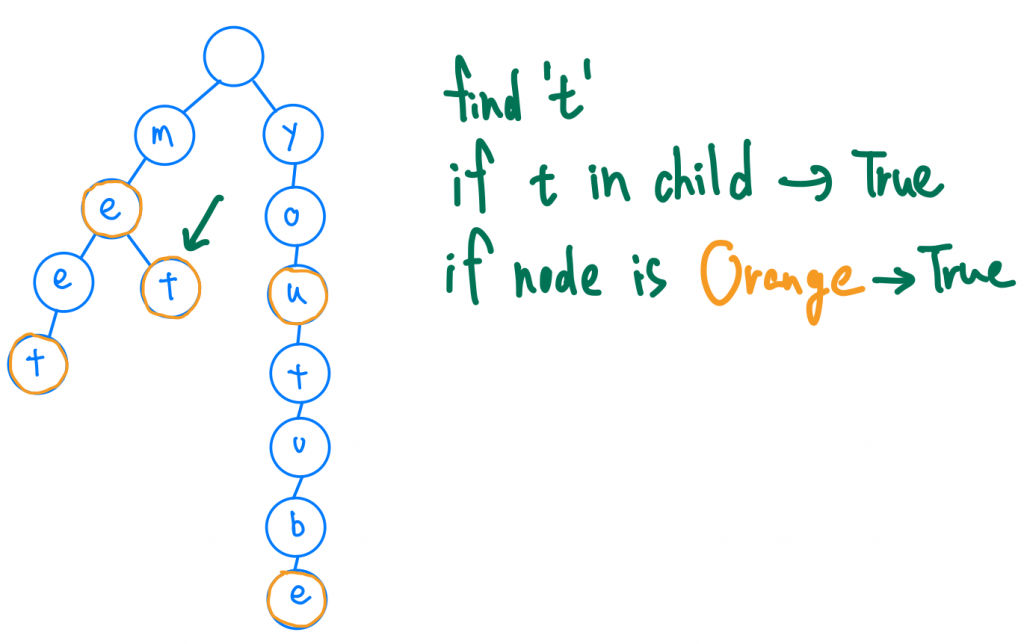
找不到的情況

大家可以比對上面的圖，大致上有兩種情況我們就可以判定這個單字不存在我們的prefix tree。

• 情況一: 搜尋的字母不在HashMap裡面，這種情況相對單純也好理解。
• 情況二: 以上面圖片為例，如果我要搜尋mee，其實mee在我prefix tree裡面是存在的，但是我們可以發現mee的最後那個e他的節點不是橘色，那就代表他不是單字的最尾巴囉。

結論

今天是對於資料結構的最後一講，當然還有很多很特別的資料結構，但我的經驗是，大家只要先把這幾天講到的資料結構好好弄懂，就可以處理大概八成以上的問題了，謝謝各位讀者們陪伴我走到這裡，明天開始會進入演算法的部分，也希望大家可以好好期待一下啦。